Формальные модели безопасности управления доступом. Модель Биба, Белла-ЛаПадулы
Формальные модели безопасности управления
доступом
При построении
систем с жесткими требованиями к защите данных очень важны гарантии
безопасности, иногда они оказываются даже более важными, чем
функциональная полнота или производительность. В некоторых случаях
недостаточно простой констатации того, что
система обеспечивает высокий уровень безопасности, нужна 100%-ная гарантия. Как ее обеспечить? Никакое самое тщательное
тестирование не может доказать, что система всегда
будет находится в безопасном состоянии. Заказчикам требуются гарантии. В такой
общей постановке задача вряд ли является разрешимой, но для некоторых частных
случаев политики управления доступом решение было найдено. А именно, были
разработаны математические модели, которые гарантировали безопасность с
математической точностью.
Суть модели – это
абстрактное представление политики. Неформальные понятия «пользователи»,
«программы», «файлы», «устройства», «запустить программу», «скопировать файл»
отображаются в виде абстрактно
определенных элементов модели «объект», «субъект», «операция читать». Затем для этих абстрактных объектов
формулируются математически определенные правила, которые отражают те концепции
и принципы функционирования системы, высказанные в политике безопасности. Имея
формальную модель политики управления доступом, для которой математически доказана
безопасность, можно на ее основе строить реальную техническую систему, начиная
с выработки технических требований и разработки архитектуры, заканчивая
написанием кода программ.
Модели
на основе конечного автомата
Модели на
основе автоматов (state machine models) являются концептуально простым и универсальным способом отображения работы
реальных систем разного типа. Автомат – это абстрактный математический объект,
который определяется начальным
состоянием Q0, множеством
состояний {Q}, множеством входных воздействий (x} и функцией
переходов F. Конечный автомат имеет конечное
множество состояний. Автомат является
детерминированным, если у него детерминированная (а не вероятностная) функция
переходов. Функция переходов вычисляет новое состояние автомата Qn+1 по заданному текущему состоянию Qn и входному воздействию xn:
Qn+1= F(Qn, xn).
Пусть мы хотим
описать в виде автомата систему
управления доступом, концепции которой определены в некоторой политике безопасности.
Для отображения
неформальных понятий, которыми оперирует политика безопасности, в модели используются абстрактные элементы - субъекты и объекты. Их
состояния характеризуются набором
атрибутов, принимающих значения из некоторого конечного множества,
определенного для этой модели (например, значений разрешений на доступ).
В каждый момент
времени автомат находится в одном из своих возможных состояний, каждое из
которых определяется конкретным сочетанием состояний всех составляющих его элементов. Поскольку
число элементов и их атрибутов конечно, то конечно и число возможных комбинаций
их состояний, а значит, конечно число состояний автомата. В общем случае среди
множества возможных состояний есть как безопасные, так и небезопасные. Состояние считается безопасным, если оно
безопасно с точки зрения используемой в данной модели политики безопасности. То
есть, если в политике безопасности определено понятие несанкционированного
доступа, то состояние системы, при котором возможен несанкционированный доступ,
является небезопасным.
Переход из одного состояния в другое происходит в соответствии с функцией
переходов в зависимости от текущего состояния и значения входного
воздействия. Входными воздействиями в
модели управления доступом могут являться операции изменения атрибутов объектов
и субъектов (например, в результате выполнение некоторой операции субъекта над
объектом). Учитывая конечность
состояний автомата и конечность множества
значений входных воздействий, теоретически можно провести тестирование
автомата, заключающееся в выполнении всех возможных переходов.
Если начальное
состояние является безопасным (всем атрибутам присвоены «правильные» начальные
значения) и функция переходов автомата сконструирована так, что при поступлении
любых возможных входных воздействий осуществляется переход только в безопасное
состояние, то такой автомат моделирует
безопасную систему. Такой вывод может быть сделан, например, в результате
программного моделирования соответствующим образом определенного автомата.
Модель
Белла-ЛаПадулы
Модель Белла-ЛаПадулы (Bell-LaPadula model), известная также как модель “no read up,
no write down”[1], была разработана в 1975 году Дэвидом Беллом и Леонардом ЛаПадулой в ответ на запросы военных и правительственных
организаций США в предоставлении им систем, гарантированно обеспечивающих
высокий уровень безопасности систем для хранения классифицированных данных. Эта
модель отражает политику безопасности, основанную на концепции мандатного
доступа, когда разрешение доступа определяется соотношением уровня допуска
пользователя и уровня конфиденциальности документа.
Для
математического доказательства
безопасности модель Белла-ЛаПадулы использует концепцию конечных автоматов.
На основе текущей
политики безопасности в модели Белла-ЛаПадулы каждому
субъекту и каждому объекту назначаются собственные уровни секретности. Уровни
секретности образуют иерархию от самого высокого до самого низкого. Для
предоставления доступа к объекту уровень секретности субъекта сравнивается с
уровнем секретности объекта.
В модели Белла-ЛаПадулы под безопасностью понимается такое состояние
системы, при котором обеспечивается конфиденциальность
информации, то есть такое состояние системы (субъектов и объектов), при котором
исключается несанкционированный доступ.
В качестве
входных воздействий на систему выступают операции доступа субъектов «читать» и
«записывать». В результате этих воздействий система может переходить как в
безопасные состояния, так и в небезопасные. Например, если в результате
выполнения какой-либо операции данные становятся доступными для субъектов с
более низким допуском (стал возможен несанкционированный доступ), то это
означает, что система перешла в небезопасное состояние.
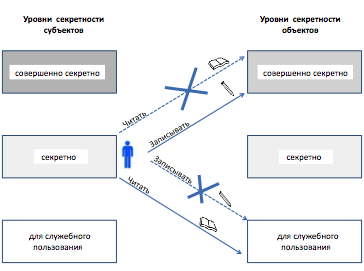
Рис.6.11. Правила
модели Белла-ЛаПадулы
Ставится задача
предложить такие правила управления доступом, при которых система всегда
переходила бы только в безопасные состояния. Такие правила формулируются в
рамках модели в виде двух свойств (рис.6.11).
· Простое свойство безопасности (The Simple Security Property) - субъекту данного уровня секретности запрещено
выполнять операцию «читать» по отношению к объектам более высокого уровня секретности (правило "no read up"). Это
свойство является интуитивно понятным, действительно, если у вас допуск
«секретно», то вам не позволено читать
документы с грифом «совершенно секретно».
· *-Свойство (The *-property) - субъекту
данного уровня секретности запрещено выполнять операцию «записывать» по
отношению к объектам более низкого уровня
секретности (правило "no write down").
Если пользователь
системы, обладающий высоким уровнем допуска, запишет некоторые данные (возможно
имеющие уровень секретности, равный его собственному) в объект с более низким
уровнем секретности, то они могут стать доступными субъекту с более низким, чем
разрешено политикой безопасности, уровнем допуска. Следование этому свойству исключает
возникновение ситуаций, подобных ситуации с «Троянским конем», которая
обсуждалась в разделе «Дискреционный метод управления доступом».
С другой стороны,
субъект может безопасно записать свои данные «наверх», туда, где к этой
информации гарантированно получат доступ только субъекты с более высоким, чем у
него уровнем секретности.
Модель
Биба
Модель Биба (Biba),
предложенная Кеннетом Биба в 1977 году, также
является формальной моделью безопасного управления доступом, однако под
безопасностью в этом случае понимается целостность.
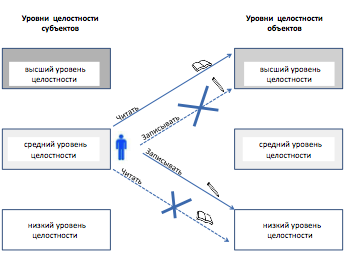
Рис. 6.12. Правила модели Биба.
Так же, как и
модель Белла-ЛаПадулы, модель Биба
(рис. 6.12) оперирует субъектами и объектами, которые также разбиваются на
иерархически организованные уровни. Но вместо уровней секретности здесь
вводятся уровни целостности. Чем выше уровень целостности объекта (например,
документа), тем более он
заслуживает доверия, тем выше
вероятность, что он содержит точные данные, тем строже правила, допускающие
субъекты к работе с этими данными. Чем выше уровень, к которому отнесен
субъект, тем больше ему доверяют, в том числе по возможностям модификации
информации, содержащейся в объектах.
Субъекты
выполняют над объектами операции «читать» и «записывать».
Модель Биба определяет два правила, при соблюдении которых система
гарантированно будет находится в безопасном состоянии.
· Простая аксиома целостности (The Simple Integrity Axiom) - субъекту данного уровня целостности запрещено
выполнять операцию «читать» по отношению к объектам более низкого уровня целостности (правило "no read down").
Субъект, читая данные из объекта, характеризуемого более низким
уровнем целостности, рискует «испортить» данные своего уровня, сделать их менее
достоверными, поэтому такие операции должны быть запрещены. Зато он может
читать проверенную, более достоверную информацию с более высоких уровней.
Аксиома
*-целостности (The *-Integrity Axiom) – субъекту данного уровня целостности запрещено выполнять операцию
«записывать» по отношению к объектам более высокого уровня целостности (правило "no write up").
Субъект, доверие к которому ограничивается некоторым уровнем
целостности, не должен иметь возможность записывать данные в объекты более
высокого уровня, так как он сможет внести в них искажения, неточности и тем
самым снизить безопасность системы. Поток данных субъекта, направленный «вниз»,
не может ухудшить степень целостности
объектов, имеющих более низкий уровень целостности.Как
видим, правила модели Биба, направленные на
обеспечение целостности данных, прямо противоположны правилам модели Белла-ЛаПадулы,
гарантирующим конфиденциальность данных. Помимо этих двух моделей разработаны
также другие формальные модели
безопасности, в частности, модели Clark–Wilson, Take-Grant, Graham-Denning.